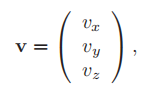《Real

您所在的位置：网站首页 › eye edition中文翻译 › 《Real

《Real

2024-07-04 08:19| 来源: 网络整理| 查看: 265

为了追赶同事（或者在公司装X），不得不开始啃RTR4（滑稽）

如题，用笨办法硬上，就是莽！

然后是概括一下每小节大致内容，最后翻译全文。

这样把全书过一遍的话应该能算认真读完了吧……

全文翻译，逐字逐句。图文并茂，绝无遗漏。

关键词已附上英文原文，部分为了通顺，采用意译。配合原书观看，风味更佳！

水平有限，尽力而为。若有建议，不胜感激！

顺便吐槽一下：知乎上看到2018年初有人接手了本书第四版翻译工作，这都快两年了，连个音信都没有……

最后还是得靠自己！

实时渲染（第四版）Real-Time Rendering (Fourth Edition) 第1章引言 Chapter 1 Introduction

实时渲染（Real-time rendering）指的是在计算机上快速生成图像。它是计算机图形学中最具交互性的领域。首先一幅图像显示在屏幕上，然后观察者做出动作与反应，并且其动作反馈会影响接下来的生成内容。由于这种反馈、渲染的循环速度足够快，观察者就不会只看到独立的图像，而是会沉浸在这种动态过程中。

图像显示速度可以用帧每秒(Frames Per Second, FPS)或者赫兹(Hz)来衡量。在每秒1帧的情况下，几乎没有交互的感觉。用户会痛苦地等待下一张新图像的到来。在 6 FPS 的情况下，交互感开始增强。视频游戏会要求 30、60、72 甚至更高的 FPS；在这种速度下，用户的注意力会集中于具体的动作与反应。

电影放映机以 24 FPS 来显示，但是会用一个快门系统(Shutter System)去让每帧显示 2 ~ 4 次以防止闪烁。这种刷新率与之前的显示率需要区分开，刷新率用赫兹 (Hz) 表示。一个每帧显示3次的快门具有 72 赫兹的刷新率。（注: 24x3=72）此外，液晶显示器（LCD）也是要将刷新率与显示率区分开。

以 24 FPS 来观看屏幕上的图像也许是可以接受的，但是高帧率对于缩小用户反应时间是很重要的。像15毫秒这样短的时间延迟就会放慢并干扰到用户的交互 [1849]。举个例子，VR头戴显示器通常要 90 FPS 以最小化画面延迟感。

实时渲染不是仅仅只有交互性。如果速度是唯一的标准，那么任何能够迅速对用户命令作出反应、并在屏幕上画些东西的应用都会符合资格。实时渲染通常指的是生成三维图像。

交互性、三维空间的某种联系是实时渲染的充分条件，但还有第三个元素也已成为定义的一部分：图形加速硬件。我们大多认为 1996 年的 3Dfx Voodoo 1 显卡的推出是消费者级三维图形领域的真正开始 [408]。随着这个市场的飞速发展，每台电脑、平板电脑和手机现在都内置了图形处理器。图 1.1 和 1.2 展示了硬件加速实现实时渲染的一些优秀例子。

图1.1 来自极限竞速7 (Forza Motorsport 7) 的一个镜头。（图片由微软 Turn 10 工作室提供）

图1.2 《巫师3》（The Witcher 3）中鲍克兰（Beauclair）的渲染图。（CD PROJECT®，The Witcher® 是CD PROJEKT Capital Group 的注册商标。由CD PROJEKT S.A. 开发的巫师游戏(The Witcher Game©) 由 CD PROJEKT S.A. 保留所有权利。巫师游戏是基于Andrzej Sapkowski 的小说改编。所有其他版权和商标均为其各自所有者的财产。）

图形硬件的进步推动了交互计算机图形领域研究的爆炸式增长。本书中我们将专注于提高速度与改进图像质量的方法，同时也会讲到加速算法、图形API的特色和局限性。本书中我们不会深入地涵盖每一个主题，我们的目标是提出关键概念和术语，解释该领域中最可靠和最实用的算法，并提供一些方向指南让读者去获取更多信息。我们尝试提供这些工具能以便让读者更好地理解这个领域，也希望证明读者值得花时间与精力来读这本书。

引用：

[1849] Watson, Benjamin, and David Luebke, “The Ultimate Display: Where Will All the Pixels Come From?” Computer, vol. 38, no. 8, pp. 54–61, Aug. 2005. Cited on p. 1, 808, 817

[408] Eccles, Allen, “The Diamond Monster 3Dfx Voodoo 1,” GameSpy Hall of Fame, 2000. Cited on p. 1

1.1 内容概览 Contents Overview

以下是对本书各章节的简要概述。

第2章，图形绘制流水线（Chapter 2, The Graphics Rendering Pipeline）

实时渲染的核心是一系列步骤，这些步骤将场景的数学描述转换成我们能看到的东西。

第3章，图形处理单元（Chapter 3, The Graphics Processing Unit）

现代GPU使用固定功能和可编程单元的组合来实现渲染管线(Rendering Pipeline)的各个阶段。

第4章，变换（Chapter 4, Transforms）

变换是操纵对象的位置、方向、大小、形状，相机的位置和视图的基本工具。

第5章，着色基础（Chapter 5, Shading Basics）

无论是写实（realistic）还是风格化（stylized），我们都会先讨论材质和光源的定义，还有它们是如何呈现出我们期望的表面外观（appearance）。其他一些表面外观相关的话题也会在此章节介绍，例如通过抗锯齿（也称反走样，Antialiasing）、透明度(Transparency)、伽马校正（Gamma Correction）来提供更高质量的图像。

第6章，纹理化（Chapter 6, Texturing）

实时渲染最为强大的工具之一就是能够快速访问以及在表面(Surfaces)显示图像。这个过程被称为纹理化(Texturing)，我们有很多不同的方法来应用它。

第7章，阴影（Chapter 7, Shadow）

在场景中添加阴影可以提高真实感和理解力。本章介绍了目前比较流行的快速计算阴影的算法。

第8章，光与颜色（Chapter 8, Light and Color）

在实现基于物理的渲染之前，我们首先需要了解如何去量化光和颜色。在物理渲染过程完成后，我们需要将得到的数量值显示出来。本章会涵盖两个话题，计算屏幕参数（accounting for the properties of the screen）和观察环境（viewing environment）。

第9章，基于物理的着色（Chapter 9, Physically Based Shading）

我们会从头开始建立对基于物理着色模型的理解。本章会从物理现象背后的规律讲起，涵盖大量的渲染材质的模型，并且会在最后提出一个方法，此方法可以用来混合材质，对材质进行过滤以避免锯齿（走样），并且保持原有的表面外观。

第10章，局部光照（Chapter 10, Local Illumination）

本章探索了描绘更精细光源的算法。在表面着色时我们会考虑到光是由具有特别形状的物理对象所发射出的。

第11章，全局光照（Chapter 11, Global Illumination）

模拟光源与场景之间多重交互的算法大大提升了图像的真实感。我们会讨论环境和方向光遮挡，在漫反射和高光表面上渲染全局光照效果的实现方法，另外还有一些有前景的统一方法。

第12章，图像空间特效（Chapter 12, Image-Space Effects）

图形硬件擅长快速的图像处理。本章我们首先会讨论图像滤波（Image filtering）和重投影技术（reprojection techniques），然后我们会探讨几种常用的后处理效果：镜头光晕（lens flares）、动态模糊（motion blur）和景深（depth of field）。

第13章，除多边形之外（Chapter 13, Beyond Polygons）

三角形（Triangles）并不总是描述对象的最快或最真实的方式。基于使用图像（images）、点云（point clouds）、体素（voxels）和其他采样集的交替表现都有其各自的优点。

第14章，体积和半透明渲染（Chapter 14, Volumetric and Translucency Rendering）

本章将聚焦于体积材质呈现以及其与光源相互作用的理论与实践。模拟的范围将从大尺度的大气层效果（large-scale atmospheric effects）到细的头发纤维内的光线散射（light scattering）。

第15章，非真实感渲染（Chapter 15, Non-Photorealistic Rendering）

试图使场景看起来更逼真（realistic）只是渲染场景方法中的一种而已。本章我们会探讨一下其他的渲染风格，如卡通阴影和水彩画效果。此外，线框（line）和文本（text）生成技术也会在本章讨论。

第16章，多边形技术（Chapter 16, Polygonal Techniques）

几何数据来源广泛，有时需要进行修改以便渲染得快速、准确。本章将会从多方面介绍多边形数据的呈现和压缩。

第17章，曲线和曲面（Chapter 17, Curves and Curved Surfaces）

更复杂的曲面表示提供了一些优势，例如能够在图像质量和渲染速度之间进行权衡、更紧凑的描绘以及平滑的曲面生成。

第18章，管线优化（Chapter 18, Pipeline Optimization）

一旦应用程序运行并使用了高效的算法，就可以使用各种优化技术使其变得更快。本章讨论的主题是怎样找到性能优化瓶颈（bottleneck）并如何去解决它。此外，本章还讨论了多进程（Multiprocessing）的相关内容。

第19章，加速算法（Chapter 19, Acceleration Algorithms）

在你成功运行程序之后，就让它运行得更快吧！本章涵盖了各种形式的剔除（Culling）和细节层次渲染（LOD, Level Of Detail）。

第20章，高效着色（Chapter 20, Efficient Shading）

场景中的大量灯光会大大降低性能。另外，在确定表面片元（Fragment）是否会显示之前就进行完全的着色计算，也是性能浪费的一大来源。我们探索了一系列的方法来解决前边这些问题和一些其他低效的着色操作。

第21章，虚拟现实与增强现实（Chapter 21, Virtual and Augmented Reality）

这些领域有着特殊的挑战和技术，要求高效、快速、稳定地生成真实的图像。

第22章，相交测试方法（Chapter 22, Intersection Test Methods）

相交测试（Intersection testing）对于渲染、用户交互和碰撞检测非常重要。本章将深度涵盖一系列最有效的通用几何相交测试算法。

第23章，图形硬件（Chapter 23, Graphics Hardware）

这里的重点是一些组件（Components），如颜色深度（color depth）、帧缓冲区（framebuffers）和基本架构类型（basic architecture types）。本章给出了一个典型GPU的实例分析。

第24章，展望未来（Chapter 24, The Future）

猜猜看未来有啥？（我们接着写）

1.2 符号和定义 Notation and Definitions

首先，我们将解释这本书中使用的数学符号。为了更多地对本节中使用的许多术语进行全面的解释，请在 realtimerendering.com 上获取线性代数的附录。

1.2.1 数学符号 Mathematical Notation

表1.1 总结了我们将使用的大多数数学符号。一些概念也将在这里详细描述。

需要注意的是，表中的规则有一些例外，主要是使用在文献中已经非常明确建立的符号来表示着色方程（shading equations），例如 $\mathit{L}$ 表示辐射度（radiance）， $\mathit{E}$ 表示辐照度（irradiance）， $\sigma_{s}$ 表示散射系数（scattering coefficient）。

角度（angles）和标量（scalars）取自 $\mathit{R}$ ，即它们是实数。向量（vectors）和点（points）用粗体小写字母表示，这些分量（Components）被写作

也就是列向量格式（column vector），这是计算机图形世界中常用的格式。有些地方我们用 $\left ( v_{x}, v_{y}, v_{z} \right )$ 代替形式上更正确的 $\left ( v_{x}, v_{y}, v_{z} \right )^{T}$ ，因为前者更容易阅读。

表1.1. 本书使用的数学符号总结类型（Type）符号（Notation）例子（Examples）角度（angle）小写希腊文（lowercase Greek） $\alpha _{i},\phi ,\rho ,\eta ,\gamma _{242},\theta$ 标量（scalar）小写斜体（lowercase italic） $a,b,t,u_{k},v,w_{ij}$ 向量或点（vector or point）小写粗体（lowercase bold） $\mathbf{a},\mathbf{u},\mathbf{v}_{s},\mathbf{h}(\rho ),\mathbf{h}_{z}$ 矩阵（matrix）大写粗体（capital bold） $\mathbf{T}(t), \mathbf{X}, \mathbf{R}_{x}(\rho)$ 平面（plane） $\pi$ : 一个向量+一个标量 $\pi : \mathbf{n} \cdot \mathbf{x} + d = 0,$ $\pi_{1} : \mathbf{n}_{1} \cdot \mathbf{x} + d_{1} = 0$ 三角形（triangle）三个点（ $\Delta$ 3 points） $\Delta \mathbf{v}_{0}\mathbf{v}_{1}\mathbf{v}_{2}, \Delta \mathbf{cba}$ 线段（line segment）两个点 $\mathbf{uv}, \mathbf{a}_{i}\mathbf{b}_{j}$ 几何实体（geometric entity）大写斜体（capital italic） $\mathit{A_{OBB}},\mathit{T},\mathit{B_{AABB}}$

这里使用齐次表示法（homogeneous notation），坐标值由四个值表示 $\mathbf{v} = (v_{x}\; v_{y}\; v_{z}\; v_{w})^{T}$ ，向量是 $\mathbf{v} = (v_{x}\; v_{y}\; v_{z}\; 0)^{T}$ ，点是 $\mathbf{v} = (v_{x}\; v_{y}\; v_{z}\; 1)^{T}$ 。有时候我们只用三维向量和点，但我们会尝试避免产生歧义。对于矩阵运算，向量和点使用相同的符号是极有利的。更多信息请参见第4章有关转换（Transform）的部分。在某些算法中，使用数字索引而不是 $x,y,z$ 会更方便，例如 $\mathbf{v} = (v_{0}\; v_{1}\; v_{2})^{T}$ 。向量和点的所有这些规则也适用于二维向量。在这种情况下，我们只需简单地跳过三维向量的最后一个分量即可。

矩阵（Matrix）值得多说几句。常用的矩阵大小为 2×2、3×3 和 4×4。我们将复习一下书写3×3矩阵 $\bg_black \mathbf{M}$ 的方式，并且很容易将此过程扩展到其他大小的矩阵。 $\mathbf{M}$ 的（标量）元素表示为 $m_{i j}$ ， $0\leq \left ( i,j \right )\leq 2$ ，其中 $i$ 表示行（row）， $j$ 表示列（column），如公式1.1所示：

$\mathbf{M}=\begin{pmatrix} m_{00} &m_{01} &m_{02} \\ m_{10} &m_{11} &m_{12} \\ m_{20} &m_{21} &m_{22} \end{pmatrix} \;\;\;\;(1.1)$

对于 3×3 矩阵，公式1.2 中使用了以下符号，用于从矩阵 $\mathbf{M}$ 分离向量： $m_{,j}$ 表示第 $j$ 列向量， $m_{i,}$ 表示第 $i$ 行向量（以列向量形式）。与向量和点一样，也可以使用 $x,y,z$ （有时用 $w$ ）对列向量进行索引，如果这样更方便的话：

$\mathbf{M}=\left (\; m_{,0} \; m_{,1} \; m_{,2} \;\right ) =\left (\; m_{x} \; m_{y} \; m_{z} \;\right ) = \begin{pmatrix} m_{0,}^{T}\\ m_{1,}^{T}\\ m_{2,}^{T} \end{pmatrix}\;\;\;\;(1.2)$

平面记为 $\pi : \mathbf{n} \cdot \mathbf{x} + d = 0$ 其中包含其数学公式、平面法线 $\mathbf{n}$ 和标量 $d$ 。法线是描述平面面向哪个方向的向量。更一般地（例如对弯曲表面），法线描述了表面上特定点的指向方向。对于一个平面来说，同一法线恰好适用于该平面的所有点。 $\pi$ 是平面的常用数学符号。平面 $\pi$ 将空间划分为正半空间 $\mathbf{n} \cdot \mathbf{x} + d 0$ 和负半空间 $\mathbf{n} \cdot \mathbf{x} + d 0$ 。所有其他点都位于该平面上。

三角形可以由三个点 $v_{0}$ ， $v_{1}$ 和 $v_{2}$ 定义，并由 $\Delta \mathbf{v}_{0}\mathbf{v}_{1}\mathbf{v}_{2}$ 表示。

表1.2 列出了一些其他的数学运算符及其表示法。点乘（dot），叉乘（cross），行列式（determinant）和长度运算符（length operators）在 realtimerendering.com 上可下载的线性代数附录中进行了说明。转置运算符（transpose operator）将列向量转换为行向量，反之亦然。因此，可以将列向量缩写为 $\mathbf{v} = (v_{x}\; v_{y}\; v_{z})^{T}$ 。Graphics Gems IV 中引入的运算符4（ $^{\perp }$ ）是二维向量上的单目运算符。使该算符作用于向量 $\mathbf{v} = (v_{x}\; v_{y})^{T}$ 可以得出垂直于 $\mathbf{v}$ 的向量，即 $\mathbf{v} \perp = (-v_{y}\; v_{x})^{T}$ 。我们使用 $\left | a \right |$ 表示标量a的绝对值，而 $\left | \mathbf{A} \right |$ 表示矩阵 $\mathbf{A}$ 的行列式。有时，我们也使用 $\left | \mathbf{A} \right | = \left | \mathbf{a}\;\mathbf{b}\;\mathbf{c} \right |=det(\mathbf{a},\mathbf{b},\mathbf{c})$ ，其中 $\mathbf{a}$ ， $\mathbf{b}$ 和 $\mathbf{c}$ 是矩阵 $\mathbf{A}$ 的列向量。

表1.2 一些数学运算符的符号运算符（Operator）描述（Description）1: $\cdot$ 点积（dot product）2: $\times$ 叉积（cross product）3: $\mathit{\mathbf{v}^{T}}$ 向量 $\mathbf{v}$ 的转置4: $^{\perp }$

单目垂直点积运算符（the unary, perp dot product operator）

5: $\left | \;\cdot\; \right |$ 矩阵的行列式（determinant of a matrix）6: $\left | \;\cdot\; \right |$ 标量的绝对值（absolute value of a scalar）7: $\left \| \;\cdot\; \right \|$ 范数（模和长度是它的特例）（length (or norm) of argument）8: $x^{+}$ x最小值限制为0（clamping x to 0）9: $x^{\mp }$ x值限制在0和1之间（clamping x between 0 and 1）10: $n!$ 阶乘（factorial）11: $\begin{pmatrix} n\\ k \end{pmatrix}$ 二项式系数（binomial coeffiffifficients）

注：the unary, perp dot product operator 没找到对应的正式中文翻译，在 mathworld.wolfram.com 查得该运算的详情如下，但和原书中提到的运算是不同的（写法也不同）。如果有了解的同学麻烦告知一下。

运算符8（ $x^{+}$ ）和9（ $x^{\mp }$ ）是限制（clamping）运算符，通常用于着色计算中。运算符8（ $x^{+}$ ）将负值限制为0：

$x^{+} = \left\{\begin{matrix} x,\;\mathrm{if} \;x0,\\ \;\;0, \; \mathrm{otherwise}. \end{matrix}\right.\;\;\;\;(1.3)$

运算符9（ $x^{\mp }$ ）将值限制在0和1之间：

$x^{+} = \left\{\begin{matrix} 1,\;\mathrm{if} \;x1,\\ \;\;x, \; \mathrm{if}\;0x1, \\0,\;\mathrm{otherwise}.\end{matrix}\right.\;\;\;\;(1.4)$

第10个运算符，阶乘，定义如下，注意 $0!=1$ ：

$n!=n(n-1)(n-2)\cdot \cdot \cdot 3\cdot 2\cdot 1.\;\;\;\;(1.5)$

如公式1.6 所示，定义第11个运算符，即二项式因子：

$\begin{pmatrix} n\\ k \end{pmatrix}=\frac{n!}{k!(n-k)!}\;\;\;\;(1.6)$

表1.3 一些特殊数学函数的符号函数（Function）描述（Description）1: $atan2(y,x)$ 二值反正切（two-value arctangent）2: $log(n)$ n 的自然对数（natural logarithm of n）

进一步地，我们将平面 $x=0$ ， $y=0$ 和 $z=0$ 称为坐标平面（coordinate planes）或轴对齐平面（axis-aligned planes）。 $\mathbf{e}_{x}=(1\;\;0\;\;0)^{T}$ ， $\mathbf{e}_{y}=(0\;\;1\;\;0)^{T}$ 和 $\mathbf{e}_{z}=(0\;\;0\;\;1)^{T}$ 的轴称为主轴（main axes）或主轴方向，它们分别单独称为x轴（x-axis），y轴（y-axis）和z轴（z-axis）。这组轴通常称为标准基（standard basis）。除非另有说明，我们将使用正交基（orthonormal basis，由相互垂直的单位向量组成）。

包含a和b以及两者之间的所有数字的范围的表示法是 [a, b] 。如果我们想要a和b之间的所有数字，而不是 a 和 b 本身，那么我们写 (a, b) 。也可以将它们组合起来，例如 [a, b) 表示 a 和 b 之间的所有数字，包括 a 但不包括 b 。

本书中将经常使用C数学函数 $atan2(y,x)$ ，因此需要引起注意。它是数学函数 $arctan(x)$ 的扩展。它们之间的主要区别是 $-\frac{\pi}{2} arctan(x)\frac{\pi}{2}$ 与 $0 \leq atan2(y,x) 2\pi$ ，并且在后一个函数中添加了一个额外的参数。 $arctan$ 的常见用法是计算 $arctan(y/x)$ ，但是当x = 0时，会有除以零的错误。 $atan2(y,x)$ 的额外参数就避免了这种情况。

在本书中，符号 $log(n)$ 始终表示自然对数 $log_{e}(n)$ ，而不是以10为底的对数 $log_{10}(n)$ 。

我们使用右手坐标系，因为这是计算机图形学领域中三维几何图形的标准系统。

颜色由三维向量表示，例如（红色，绿色，蓝色），其中每个元素的范围为 [0, 1] 。

1.2.2 几何定义 Geometrical Definitions

几乎所有图形硬件使用的基本渲染图元（Rendering Primitives，也称为绘图图元）是点（points），线（lines）和三角形（triangles）。（1）

在本书里，我们将几何实体的集合称作模型（model）或对象（object）。场景是模型的集合，其中包括要渲染的环境中包含的所有内容。场景还可以包括材质描述（material descriptions），光照（lighting）和视图规格（viewing specififications）。

举个例子，对象可以是汽车，建筑物甚至直线。在实践中，对象通常由一组绘图图元组成，但并非总是如此。一个对象可能具有较高的几何表示形式，例如贝塞尔曲线（Bezier curves），曲面（surface），细分曲面（subdivision surfaces）。另外，对象可由其他对象组成，例如汽车的对象包括四个门对象，四个车轮对象等等。

作者注：

(1) 我们知道的唯一例外是可以绘制球体的 Pixel-Planes [502] 和可以绘制椭圆体的 NVIDIA NV1 芯片。

引用：

[502] Fuchs, H., J. Poulton, J. Eyles, T. Greer, J. Goldfeather, D. Ellsworth, S. Molnar, G. Turk, B. Tebbs, and L. Israel, “Pixel-Planes 5: A Heterogeneous Multiprocessor Graphics System Using Processor-Enhanced Memories,” Computer Graphics (SIGGRAPH ’89 Proceedings), vol. 23, no. 3, pp. 79–88, July 1989. Cited on p. 8, 1026

1.2.3 着色 Shading

遵循公认的计算机图形学用法，在本书中，术语“着色”（Shading），“着色器”（Shader）及相关的词汇用于指两个不同但相关的概念：分别是计算机生成的视觉外观（例如，“着色模型 Shading Model”，“ 着色方程 Shading Equation”，“卡通着色 Toon Shading”）或者渲染系统的可编程组件（例如“顶点着色器 Vertex Shader”，“着色语言 Shading Language”）。两种情况下，预期含义均可从上下文中清楚看出。

进一步阅读和参考资料 Further Reading and Resources

我们可以为您推荐的最重要资源是本书的网站：realtimerendering.com。它包含每个章节的最新信息和网站链接。实时渲染领域正在变化的速度也是实时的。在本书中，我们尝试着眼于那些不太可能过时的基本概念和技术。而在网站上，我们有机会介绍与当今一线软件开发人员有关的信息，并且我们有能力使其保持最新状态。

（本章完）

下一章节：第2章图形渲染管线（上）2.1 ~ 2.3

【本文地址】

公司简介

联系我们